MATEMÁTICAS II
BLOQUE VI: DESCRIBES LAS RELACIONES TRIGONOMÉTRICAS PARA RESOLVER TRIÁNGULOS RECTÁNGULOS.
BLOQUE VII: APLICAS FUNCIONES TRIGONOMÉTRICAS.
RAZONES TRIGONOMÉTRICAS
Función Seno ( Sen):
La Función Seno nos describe la relación existente entre Lado Opuesto sobre la
Hipotenusa. Su simbología es la siguiente:

2. Función Coseno ( Cos):
La Función Coseno describe la relación entre Lado Adyacente sobre
Hipotenusa. Su simbología es la siguiente:

3. Función Tangente ( Tan):
Ésta Función nos representa la relación entre Lado Adyacente sobre
Hipotenusa. Su simbología es la siguiente:

También tenemos las Funciones que son inversas a las anteriores:
4. Función Cotangente ( Cot):
Que describe la relación entre Lado Adyacente con Lado Opuesto:

5. Función Secante ( Sec):
Relación entre Hipotenusa sobre Lado Adyacente:

6. Función Cosecante ( CsC):
Nos muestra la relación entre Hipotenusa sobre Lado Opuesto:

Función Seno ( Sen):
La Función Seno nos describe la relación existente entre Lado Opuesto sobre la
Hipotenusa. Su simbología es la siguiente:
2. Función Coseno ( Cos):
La Función Coseno describe la relación entre Lado Adyacente sobre
Hipotenusa. Su simbología es la siguiente:
3. Función Tangente ( Tan):
Ésta Función nos representa la relación entre Lado Adyacente sobre
Hipotenusa. Su simbología es la siguiente:




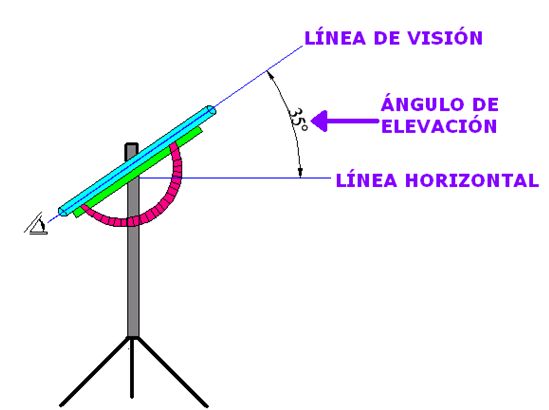
ÁNGULOS DE ELEVACIÓN Y DE DEPRESIÓN
Son ángulos formados por dos líneas imaginarias llamadas: línea
visual o línea de visión y la línea horizontal.
En estos casos, el observador se encuentra por debajo del objeto observado o bien, se encuentra por encima de dicho objeto.
Para estas mediciones se utilizan sencillos aparatos que colocados sobre un trípode ( 3 puntos determinan un solo plano) el simple giro realizado de la mirilla sobre el punto a observar nos señala los grados girados respecto a la horizontal:
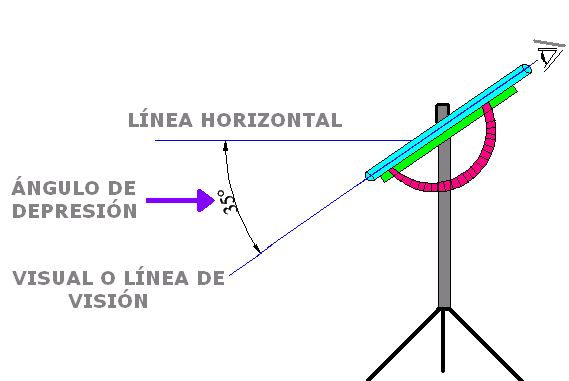
En el caso del ángulo de depresión, el observador se encuentra por encima del lugar a observar y del modo anterior su representación podemos hacerla del modo siguiente:
Ejercicio #1
Una escalera debe llegar hasta los 3 metros de altura de una pared con una inclinación de 51º respecto al suelo. ¿Qué longitud debe tener la escalera?
La figura la tienes a continuación:
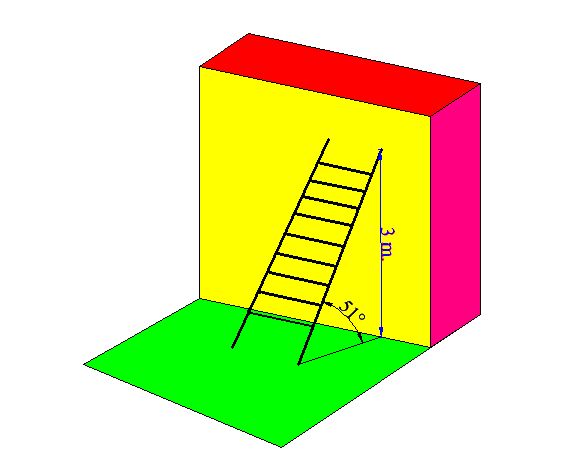
Respuesta: 3,916 m .
Solución
sen 51º 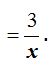
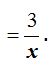
Calculamos el sen 51º = seno(51*pi()/180) = 0,7771
Sustituyendo valores:
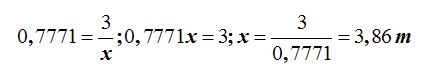
Ejercicio #2
¿Cuánto vale el coseno de 60º?
Respuesta: 0,5
Ejercicio #3
¿Cuánto vale el cos 75º?
Respuesta: 0,2588
FUNCIONES TRIGONOMÉTRICAS
Para las Funciones Trigonométricas, como se mencionó anteriormente,
haremos uso del Teorema de Pitágoras y trabajaremos con las Funciones
de Seno, Coseno y Tangente, y sus inversas, además de apoyarnos
siempre con la Calculadora.
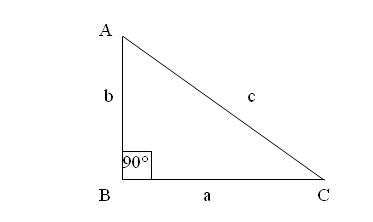
Las letras minúsculas son las que utilizamos en el Teorema de Pitágoras,
las letras Mayúsculas, en éste caso, se utilizarán para referirnos a los
Ángulos del Triángulo.


Para resolver un triángulo rectángulo es necesario encontrar los lados y los ángulos que se desconocen a través de los ya conocidos.
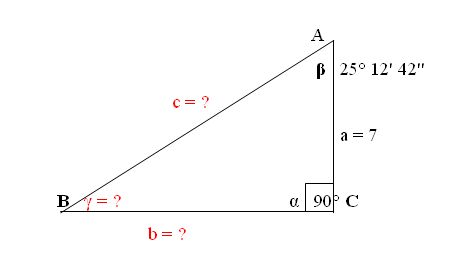
Recordemos que un Triángulo Rectángulo es aquel queestá constituido por dos lados (Opuesto y Adyacente),Hipotenusa y forma un ángulo de 90 grados (90°)En el Diagrama se simbología asignada para cada variable:
3. Ahora, empezaremos a encontrar los lados que nos hacen falta,
ya que conocemos γ, podemos encontrar el lado por medio de las funciones
Despejemos la Variable:
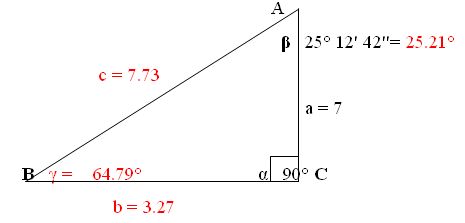
El Lado a es opuesto al ángulo γ (Sigma) Veamos un Ejemplo, nos proporcionan la siguiente información:
Revisemos la información que tenemos:
Tenemos un ángulo β equivalente a 25° 12 ' 42'',
por lo que tenemos que pasarlo a Grados;
aparte conocemos el lado c = 7 cm.
Nos piden encontrar un ángulo y dos lados,
que son los que desconocemos.

2. Conociendo β, podemos conocer γ, ya que α = 90°, así:

trigonométricas:

c Sen 64.79 ° =

Aplicamos por medio de la Calculadora La Función Seno de 64.79,
que es : 0.9047527, luego dividimos 7 ÷ 0.9047527 = 7.73 = c.
4. Ahora conociendo el valor de c, podemos aplicar el Teorema de Pitágoras:
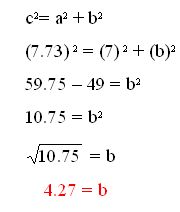
5. Quedando finalmente la gráfica así:
gracias por visitar este blog